MARI CARI TAHU BAGAIMANA PENGGUNAAN TEOREMA PYTHAGORAS PADA METEMATIKA
Banyak yang dapat kita ketahui tentang kegunaan
teorema Pythagoras. Pada bangun ruang misalkan balok, teorema Pythagoras dapat
digunakan untuk menentukan panjang diagonal sisi dan diagonal ruang. Selain
itu, teorema Pythagoras juga dapat digunakan untuk mengukur atau menentukan
jarak antara dua titik pada bidang koordinat.
A. JARAK DUA TITIK
Perhatikan gambar. Terdapat dua buah titik
yaitu titik A(x1, y1) dan titik B(x2, y2).
Jarak antara kedua titik tersebut dapat ditentukan menggunakan teorema
Pythagoras berikut.
atau
B. PANJANG DIAGONAL
Perhatikan
gambar berikut. Sebuah persegi berukuran panjang sisi (s) dan persegi panjang
mempunyai ukuran panjang (p) dan lebar (ℓ). Dengan teorema Pythagoras,panjang diagonal
kedua bangun datar tersebut dinyatakan sebagai berikut.
1.
Diagonal Persegi
2. Diagonal Persegi Panjang
C. PANJANG DIAGONAL SISI DAN DIAGONAL RUANG
Perhatikan gambar di atas. Kubus
mempunyai ukuran panjang rusuk (s), sedangkan balok
berukuran panjang (p), lebar (ℓ), dan tinggi (t).
Dengan teorema Pythagoras, panjang diagonal sisi dan
diagonal ruang kedua bangun ruang tersebut dinyatakan
sebagai berikut.
1. Panjang kubus ABCD.EFGH.
Panjang diagonal sisi:
Panjang diagonal ruang:
2. Pada balok ABCD.EFGH.
Panjang diagonal sisi:
Panjang diagonal ruang:
CONTOH
1. Perhatikan gambar balok berikut.
Tentukan:
a. Panjang diagonal sisi KM dan
b. Panjang diagonal ruang KQ.
Jawab:
a. Panjang KM
Alas balok KLMN berbentuk persegi panjang dengan panjang KL = 16 cm, dan LM = 12 cm. Oleh karena ∠KLM = 90° maka panjang KM ditentukan menggunakan teorema Pythagoras.
Panjang KM:
Jadi, panjang diagonal sisi KM = 20 cm.
b. Panjang KQ
Perhatikan segitiga KMQ siku-siku di M dengan panjang KM = 20 cm dan MQ = 15 cm. Garis KQ merupakan diagonal ruang. Panjang KQ ditentukan menggunakan teorema Pythagoras.
Panjang KQ:
Jadi, panjang diagonal ruang KQ = 25 cm.
2. Perhatikan gambar berikut.
Tentukan:
a. Panjang BE dan
b. Luas BCHE.
Jawab:
a. ∆ABE siku-siku di A.
Jadi, panjang BE = 15 cm.
b. Luas BCHE
BCHE berbentuk persegi panjang
L = p × ℓ = BE × BC = 15 × 6 = 90 cm2
Jadi, luas BCHE = 90 cm2.



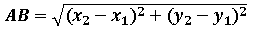














0 Response to "MARI CARI TAHU BAGAIMANA PENGGUNAAN TEOREMA PYTHAGORAS PADA METEMATIKA"
Post a Comment